Passive Dissipater Operation
- Published: January 07, 2013, By Kelly Robinson
How do passive dissipaters work with no external power source?
Passive static dissipaters like tinsel, static brushes, and ionizing cords work because the electric field that fills the space between a charged web and a nearby grounded object is stronger at corners and points. The web in Figure 1 carries charge onto the span between two grounded rollers. The tinsel must be grounded to function properly. However, a power supply is not required. With no external power, how does the tinsel neutralize the charged web?
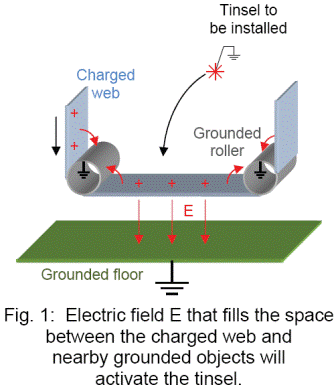
An electric field E fills the space between the charged web and nearby grounded objects. When the tinsel is installed, the electric field near the sharp tips of the tinsel will be so strong that air ionizes to form corona ions that will neutralize the web. Let’s analyze two simple geometries to see how this happens.
First, let’s take a look at the electric field between the charged web and the floor. The charged web is represented by the upper electrode in Figure 2. Charge on the web is included by applying voltage V0 to the upper electrode. The floor is modeled by the lower electrode that is grounded. The web is located distance D above the floor.
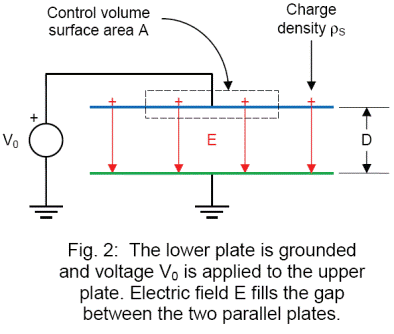
Since our web carries static charge, let’s find the electric field E in terms of the charge by enclosing the upper electrode with the control volume in Figure 2. The electric field E exiting the control volume is proportional to the static charge QINSIDE enclosed within.
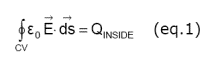
The integral in (eq. 1) is just the mathematical way to find the electric field exiting the control volume, that is the electric field E times the surface area A.

The charge QINSIDE within the control volume is the charge density r S times the surface area A.
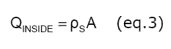
Finally, we can use (eq. 2) and (eq. 3) to find the electric field E.
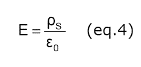
(Eq. 4) is the “parallel plate approximation” that I often use to estimate the electric field near a charged web. For example, the electric field E is estimated in (eq. 5) for a web carrying 0.5 mC/m2 of static charge, which is a low level.
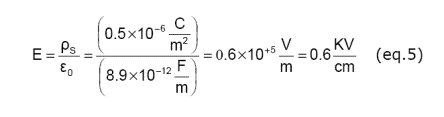
Now, an electric field of about 30 KV/cm is needed to ionize air. To work, the strand of tinsel and other passive dissipaters must intensify this nominal electric field by at least 50X.
To see how passive dissipaters intensify the electric field, let’s find the electric field in the gap between the two concentric spheres in Figure 3.
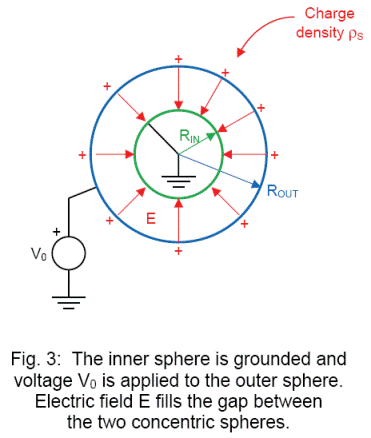
The charged web is represented by the surface of the outside sphere with radius ROUT. In the end, we’ll make ROUT so large that it might as well be flat compared with the sharp tip of the tinsel that is represented by the surface of the inner sphere with radius RIN. The tinsel is grounded and the static charge on the web is modeled by applying voltage V0 to the outer sphere.
We can find the electric field in terms of the static charge on the web just as we did before. Enclose the outer electrode with the control volume in Figure 4.
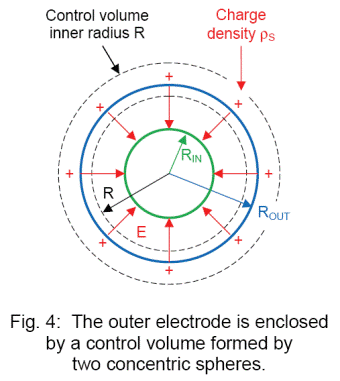
The electric field E exiting the control volume is proportional to the charge inside QINSIDE.
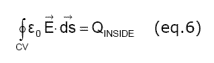
The charge inside is the charge density r S times the surface area of the outer electrode.
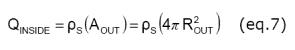
The electric field E exiting the control volume is E times the surface area of the inner surface of the control volume.
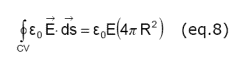
Use (eq. 7) and (eq. 8) to solve for the electric field E as a function of radius R.
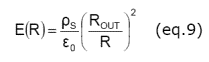
(Eq. 9) reveals how tinsel and other passive ionizers work. First, let’s check to be sure that our model results are consistent. The electric field in (eq. 9) at the surface of the charge web found for R=ROUT is just the nominal field at the surface of the web that we found using the “parallel plate” approximation in (eq. 4). Our analyses of the two model geometries find identical magnitudes of the electric field near the surface of the charged web. Consistency is good!
Next, let’s look at the value of the electric field at the surface of the sharp tip found for R=RIN.
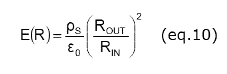
When the tips of the tinsel or the radii of the fibers in the static brush are very small, the electric field at the sharp tips is increased by a factor of (RWEB/RTINSEL)2. For a passive dissipater such a strand of tinsel, a static brush, or an ionizing cord, the radii of the sharp tips are typically about 0.001 inches (25 mm). The magnitude of the electric field at the sharp tip is estimated in (eq. 11) assuming that our web has a 1 m radius of curvature.
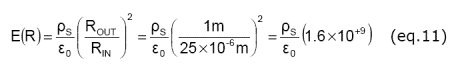
So, for passive dissipaters to operate, we needed to increase the electric field by a factor of 50X, and we find that, using reasonable assumptions, the electric field is increased by a factor of 10+9. Wow!
Well, this intensification result is extreme. Our model is extreme because the electric field from a large area of web exposed to only a single point. Of course, actual dissipaters have many sharp tips and points. In reality, passive dissipaters intensify the field by approximately 50X. When working properly, passive dissipaters are able to reduce the electric field near a charge web only to about ±0.5 KV/cm. None-the-less, field intensification is real and it is the fundamental operating principle of passive dissipaters.
Tinsel, static brushes, ionizing cords and other passive dissipaters work because the nominal electric field near a charged web is intensified at the sharp tips in the dissipaters.
I invite you to share your comments on this blog below. And, please feel free to suggest topics for future blogs.
My email address is:
Kelly.Robinson@ElectrostaticAnswers.com
Please feel free to visit my website:
www.ElectrostaticAnswers.com













