Model Behavior
- Published: June 01, 2003, By Edgar B. Gutoff, Industry Consultant
Computer modeling is a relatively new tool converters can use to improve the quality and productivity of coating and drying operations.
Computer modeling represents the coating and drying processes in mathematical language and then solves the resulting equations. It frequently involves suitably approximating or idealizing the process so the equations are as simple as possible while still giving an adequate representation of reality.
A good model may be used to optimize a new formulation, determine operating conditions for production, and help in understanding the mechanisms of defect formation. It is much easier, less expensive, and more efficient to run a model than to carry out experiments. This is especially true in coating operations, where even pilot runs tend to be relatively expensive. However, some experiments still may be needed to confirm the results of the simulation.
Models also may be used to test production conditions that may not be attainable in the pilot plant. This allows evaluating the effectiveness of new equipment before making an investment.
Experiments carried out on models may be used to develop a qualitative understanding of the system's behavior, in order to get a “feel” of how to change conditions to move the system in a desired direction. In such cases statistical designs would be run on the model, just as they are done in laboratory and pilot runs. In some cases, once this understanding is developed, the model may no longer be needed—it has served its purpose already.
Sometimes the model contains only algebraic equations, but more often the model involves differential and even partial differential equations. Frequently the equations cannot be solved analytically to give a direct answer but must be solved numerically. That means the answer—whatever we are looking for—cannot be found explicitly as equal to some combination of different variables but must be found by an involved numerical technique for each specific case. Computers are essential to find these solutions in a reasonable time period.
The Techniques
Two common techniques are used for numerical solutions: the finite difference method and the finite element method. The finite difference procedure may be illustrated by the diffusion of solvent toward the coating surface during the so-called falling rate period drying. The coating is imagined as consisting of a number of thin layers, in each of which the concentration at the central plane is assumed to be equal to the average concentration in the layer. A material balance is written for the solvent in each layer so the rate of change of solvent in each layer—the solvent concentration times the layer thickness—equals the rate of diffusion into the layer from below, minus the rate of diffusion out to the layer above. At the end of each short time interval, the new solvent concentrations are calculated, and from them the new layer thicknesses. The rate of evaporation of the solvent is equal to the rate of diffusion to the surface. Finite difference equations are relatively easy to program.
The finite element method is much more involved and may be illustrated in the calculation of the shape and velocity vectors in a coating bead in slot coating.
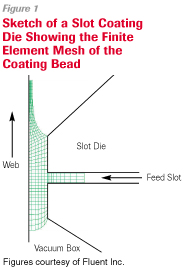 Here the coating bead of some assumed shape is divided into a number of elements, usually four sided, as illustrated in Figure 1. Smaller elements are used where pressures and velocities are changing rapidly. For each element the basic equation of fluid mechanics (the Navier-Stokes equation) is written to solve for the pressure and velocity at each corner and at some intermediate nodes.
Here the coating bead of some assumed shape is divided into a number of elements, usually four sided, as illustrated in Figure 1. Smaller elements are used where pressures and velocities are changing rapidly. For each element the basic equation of fluid mechanics (the Navier-Stokes equation) is written to solve for the pressure and velocity at each corner and at some intermediate nodes.
The program also solves for the contours of the free surface.
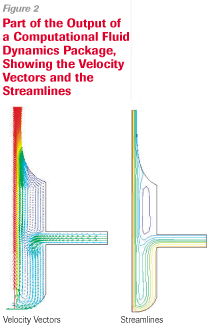 Figure 2 shows the calculated velocity vectors and the flow streamlines for this case. Both outputs in Figure 2 show a vortex, which is undesirable, has formed under the upper die lip.
Figure 2 shows the calculated velocity vectors and the flow streamlines for this case. Both outputs in Figure 2 show a vortex, which is undesirable, has formed under the upper die lip.
The equations for all the elements must be solved simultaneously, which involves a very large number of computations. Until recently supercomputers were needed. Now these computations are carried out on standard PCs.
Main Uses for Models
For coating, modeling is used to predict the regions of coating stability for new and existing products, to predict the effect of changes in the process and in solution properties, and to design coating dies. The finite element method for fluid flow is available for lease as a computational fluid dynamics package from several vendors to accomplish these tasks.
Two vendors, for example, are Fluent Inc. in New Hampshire [603-643-2600] and Flow Science Inc. in New Mexico [505-662-2636]. While these models are expensive and complex, they are much more user-friendly than they had been, and the vendors do provide training.
Drying programs are used to predict the residual solvent in the coating at the end of the dryer and the drying conditions needed to reach a given residual solvent level. They also predict the coating temperatures throughout the dryer.
Drying programs, which may be of finite difference or of finite element design, can be much smaller, simpler, less expensive, and easier to run than the computational fluid dynamics models. Several are available. One is from the author; dryer vendors also may have models available.
Edgar B. Gutoff has been consulting on coating and drying since 1988, when he left Polaroid after 28 years. He is a fellow of AIChE and IS&T, serves on the technical advisory panel of AIMCAL, and has received the Tallmadge Award for contributions to coating technology . He has co-authored two books on coating and one on statistical process control and has published more than 40 papers. Contact him at 617/734-7081; This email address is being protected from spambots. You need JavaScript enabled to view it.; coe.neu.edu/~ebgutof/
This article, along with future articles by other authors, is provided as a cooperative effort between PFFC and AIMCAL.
Authors contribute to AIMCAL's technical and education offerings, which include the association's Fall Technical Conference, Summer School, and Ask AIMCAL.




